Misuriamo indirettamente

Obiettivi

1. Conoscenza delle caratteristiche dei triangoli simili e delle proporzioni

2. Saper usare semplici formule matematiche

3. Utilizzare le operazioni matematiche

4. Utilizzare correttamente il metro e altri strumenti di misura

5. Rispettare la successione delle varie fasi esecutive

Contenuti

Gli angoli, i triangoli, caratteristiche dei triangoli simili. Applicazione di semplici formule matematiche. Concetto di proporzionalità. Ripasso e uso delle operazioni matematiche. Unità di misura lineare, multipli e sottomultipli, equivalenze. Strumenti di misura: metro lineare a nastro d’acciaio, doppio decametro, metro ultrasonico, calibro. Cronometro: unità di misura del tempo, conversione tra ore, minuti, secondi. Concetto di velocità. Valore medio. Uso di sequenze operative, necessità del rispetto temporale delle varie fasi. Conoscenza dei termini specifici.

Metodo

E’ stata proposta una attività interdisciplinare mirante alla conoscenza del fiume che attraversa la città a pochi passi dalla stessa scuola; ciò ci ha permesso non solo la conoscenza degli aspetti morfologici caratteristici, delle essenze presenti nell’alveo, ma tutta una serie di rilievi più propriamente tecnici, qui presentati.

Prima di scendere “sul campo”, occorre non solo verificare le abilità possedute dagli allievi, ma anche fornire loro gli strumenti di conoscenza che permetteranno loro, la giusta esecuzione delle misure.

Si riprende l’Unità Didattica su forma funzione (vedi Scuola e Didattica n. 5 del 1.11.2001) dove sono stati trattati gli angoli, come si misurano, i triangoli, come si calcola la somma degli angoli interni, per definire, quindi, le caratteristi dei triangoli simili, che riporteremo sul quadernone:

“Due triangoli sono simili, quando hanno gli angoli corrispondenti uguali”

“Due triangoli simili, hanno i lati corrispondenti in proporzione”

Il concetto di proporzione è stato trattato con la topografia a proposito delle “scale”; si può riproporlo e chiarirlo ulteriormente.

Si passa quindi a presentare come si valuta l’altezza di un albero.

H = altezza da misurare

D = misura della distanza albero – occhio

h = altezza sull’asta ricavata traguardando la cima dell’albero

d = misura distanza occhio - asta

Questo metodo ci permette di misurare indirettamente l’altezza di alberi, palazzi, pali elettrici e muri. La misura ricavata, non è precisa al centimetro, ma è approssimata e comunque tanto più vicina alla realtà, quanto più si eseguono con precisione, le varie fasi e misure.

Da quanto detto, precedentemente, se guardiamo il nostro disegno, i due triangoli, occhio, base e cima albero, e occhio, base e altezza asta, sono simili; perciò avranno i lati proporzionali nella seguente maniera: H / h = D / d

Dalla proporzione dei lati, ricaviamo la formula che applichiamo:

H = D * h / d

Vediamo come si procede:

1. Si prende con il doppio decametro la misura “D”, che segneremo sul terreno, abbastanza ampia, dalla base del tronco fino a dove si appoggerà il viso per traguardare con l’occhio.

2. Da questo punto, si riporta verso l’albero “d”, di misura ridotta, dove fisseremo perpendicolarmente l’asta.

3. Ora, un allievo sdraiato, con l’occhio il più vicino al terreno, traguarderà l’asta e la cima dell’albero.

4. Il ragazzo, con l’aiuto di un amico, che, sorreggendo l’asta, sposterà il suo dito lungo la sua altezza, dirà quando esso, collimerà con la parte più alta dell’albero.

5. La misura rilevata sull’asta è “h”.

6. Si applica la formula e si calcola l’altezza da trovare.

Quanto già espresso si applica per la misura di una qualsiasi larghezza non direttamente ricavabile, come una strada molto percorsa da auto, un canale, un campo da gioco…

Per il fiume si suggerisce di scegliere un tratto compreso tra argini con una larghezza abbastanza uniforme.

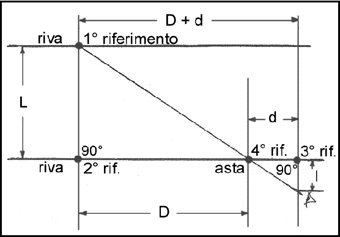
Se osserviamo bene, i due triangoli sono simili, perché sono originati da due angoli opposti al vertice, che sono uguali e hanno entrambi due angoli da 90° per costruzione. Quando due triangoli hanno due angoli uguali, anche il terzo lo é.

Perciò i lati sono fra loro proporzionali: L / l = D / d .

La formula da applicare, è: L = D * l / d

Anche qui vediamo come si procede:

1. Si individua nella riva opposta un 1° riferimento (un albero, un masso, una crepa sull’argine…) che poi traguarderemo.

2. Si segna la nostra posizione (2° riferimento) proprio davanti al 1° riferimento

3. Da questi, si prende una misura ampia, lungo la sponda, data da “D + d”, all’estremo della quale metteremo il 3° riferimento.

4. Indietreggiamo perpendicolarmente da quest’ultimo segnale, di una misura ridotta, all’estremo della quale si metterà l’operatore.

5. Un aiutante munito di asta, che cercherà di tenere perpendicolarmente al terreno, si sposta lungo il lato del fiume dove stiamo misurando, verso il 2° riferimento.

6. L’operatore che è immobile nella posizione già individuata, gli indicherà di fermarsi allorquando l’asta collimerà con in 1° riferimento nella sponda opposta.

7. Possiamo così misurare “d” e ricavare “D”.

8. Applicando la formula, ricaviamo la larghezza del tratto interessato.

Dal momento che l’analisi sul fiume procedeva, ci siamo domandati se fosse stato possibile per noi ricavarne la portata, cioè la quantità d’acqua trasportata.

Questa è data dalla velocità della corrente fluviale, moltiplicata per la sezione del tratto del corso d’acqua che stiamo misurando, per un coefficiente di rugosità, che dipende dal tipo di fondale, più o meno denso di asperità:

Q = S * V * K dove

Q = portata del fiume misurata in metri cubi al secondo

S = sezione del tratto interessato in metri quadri (larghezza del fiume per la profondità dell’acqua)

V = velocità della corrente misurata in metri al secondo

K = coefficiente di rugosità che va da 0.6 a 0,8

Per ricavare la profondità media, si provvede ad effettuare più misure di profondità per tutta la larghezza del tratto che si sta rilevando, si sommano fra loro e quindi si divide per il numero dei rilievi effettuati.

Per ricavare la velocità della corrente, abbiamo usato il metodo del galleggiante, lanciando in acqua pezzi di legna semisommersi, dei quali ricaviamo il tempo impiegato a percorrere un tratto ben delimitato e sempre lo stesso. Più legnetti, gettati in diversi punti della larghezza del fiume, ci permettono di ricavare il tempo medio. Il valore dello spazio percorso fratto il tempo impiegato ci dà la velocità.

Il fatto di usare legnetti semisommersi, ci evita di far influire eccessivamente il vento su di loro. Per il tratto, noi abbiamo scelto una zona munita di briglia, a sezione costante che ci ha facilitato il calcolo e le misurazioni cronometriche. Anche il fondale si è presentato poco rugoso, perciò abbiamo usato il coefficiente dal valore più elevato.

Tra gli strumenti conosciuti durante questa proposta didattica, ho mostrato ai ragazzi anche un recente metro ultrasonico di tipo elettronico. Nella discussione scaturita in classe è emerso che anche questo apparecchio, per valutare le distanze usa un metodo indiretto. Al momento del suo funzionamento, è percepibile il ticchettio dell’emissione degli ultrasuoni. Esso infatti emette frequenze al di sopra della frequenza udibile; queste rimbalzano sulla parete di riferimento e ritornano allo strumento dove sono rilevate. Dal momento che il suono ha una velocità di 344 metri al secondo, un microprocessore interno rivela il tempo impiegato per tale percorso, trasformandolo direttamente in metri. Qualche ragazzo lo ha giustamente paragonato, al “sonar” dei pipistrelli.

Per completare questo intervento didattico propongo la realizzazione di un piccolo strumento utilizzato dai boy scouts, per determinare le altezze degli alberi, chiamato “asta del boscaiolo” da cui prende origine.

Si tratta di un piccola asta di compensato, le cui dimensioni indicative sono 240 x 50 mm. Vi pratichiamo dei fori, iniziando da quelli più esterni; successivamente si fanno dei fori, sempre nella metà della misura precedente.

Si usa sorretta davanti al viso adattandone la distanza avanti e indietro, con la testa immobile, in modo tale da visualizzare contemporaneamente, sul foro in basso la base dell’albero, mentre sul foro in alto, la cima. Utilizzando uno dei fori intermedi, più conveniente, si visualizza sull’albero un riferimento facilmente raggiungibile; si misura la sua altezza dalla base e la si moltiplica per il denominatore del 3° foro corrispondente, trovando così l’altezza dell’albero.

E’ una piccola realizzazione pratica, facilmente realizzabile, che stimola fortemente i ragazzi.

Verifiche

Al fine di valutare, le conoscenze necessarie per poter affrontare il lavoro proposto, si assegneranno ai ragazzi dei triangoli da disegnare nel quadernone e sui quali loro dovranno ricavare gli angoli e trascrivere le caratteristiche delle figure. Inoltre si assegneranno triangoli simili. Ricavati o all’interno dello stesso triangolo, o sul prolungamento di un vertice. La corretta lettura del goniometro indicherà le caratteristiche di questo tipo di figure geometriche.

Una ulteriore verifica sarà effettuata sugli schemi proposti e disegnati nel quaderno: la corretta esecuzione delle figure, delle linee e frecce delimitatrici delle misure, della posizione delle lettere di riferimento, sulle varie annotazioni riportate.

Dopo aver eseguite alcune prove, per permettere loro di capire meglio la giusta applicazione di quanto trattato, si possono dare ai ragazzi delle altezze e larghezze da valutare, sulle quali si verificherà, il corretto rilevamento delle misure, l’uso corretto delle formule, delle operazioni da eseguire e sullo schema attinente.

Anche l’esecuzione in laboratorio, dell’asta del boscaiolo, può essere motivo di verifica.

Inoltre in classe, si valuterà la conoscenza teorica, di quanto appreso attraverso una serie di domande che riguarderanno le caratteristiche dei triangoli simili, le differenze o meno tra i due sistemi di rilevamento (altezza e larghezza), l’uso dei galleggianti semisommersi, la determinazione della velocità della corrente, sul valore medio, sulla trasformazione da metri cubi al secondo a litri al secondo, sulla velocità del suono, sul funzionamento del metro ultrasonico.

Discipline coinvolte

E’ evidente la particolare collaborazione con geometria e con matematica. Questa attività si presta in maniera particolare, a capire e a rinforzare le abilità di calcolo possedute dai ragazzi, a renderli più padroni dei vari strumenti di misure, con la relativa applicazione delle varie equivalenze collegate, delle conversioni, l’applicazione di diversi concetti. Questa attività meriterebbe perciò una effettiva collaborazione interdisciplinare.

Bibliografia

Marsilio Parolini “Il manuale dell’esploratore” Ed. Piemme 1993 Casale Monferrato

Dermot McGuigan “Energia dall’acqua…” Ed. Muzzio1980 Padova (misure di portata)

Sant’Angelo in Vado 30.12.01

Prof. Giuseppe Dini